Du kennst bereits die Methode der Punktprobe.

Damit haben wir getestet, ob ein gegebener Punkt auf dem Graph einer Funktion liegt.

Überlege, wie du diese Methode nutzen kannst, um den Streckfaktor a zu bestimmen.

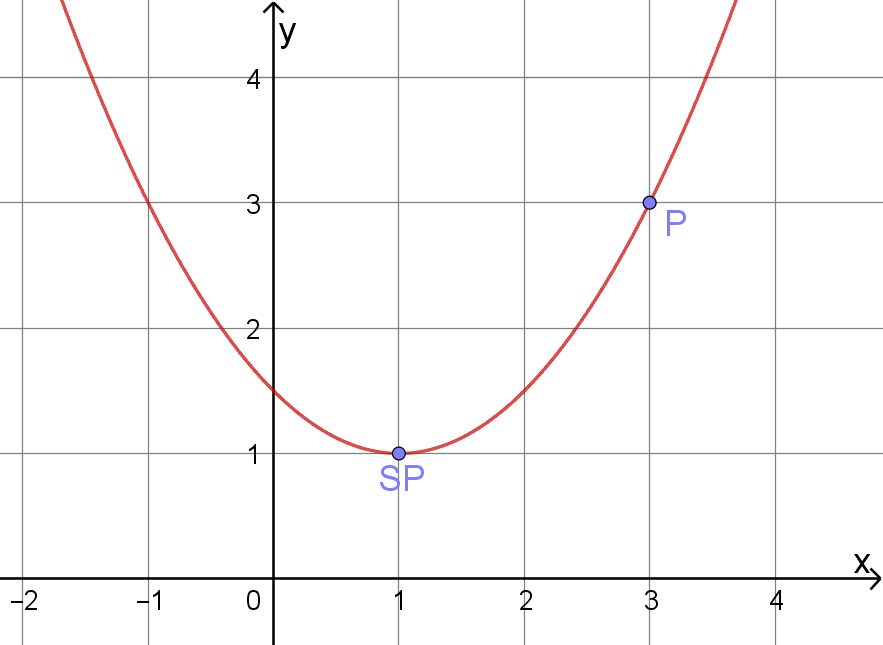
Ähnlich wie bei der Punkprobe setzen wir die Koordinaten eines Punktes in die Funktionsgleichung ein.

Nur wählen wir gezielt einen Punkt aus, von dem wir wissen, dass er auf der Parabel liegt.

Die Koordinaten des Punktes P setzen wir in die Scheitelpunktform ein. 

Dann müssen wir nur noch nach a auflösen.

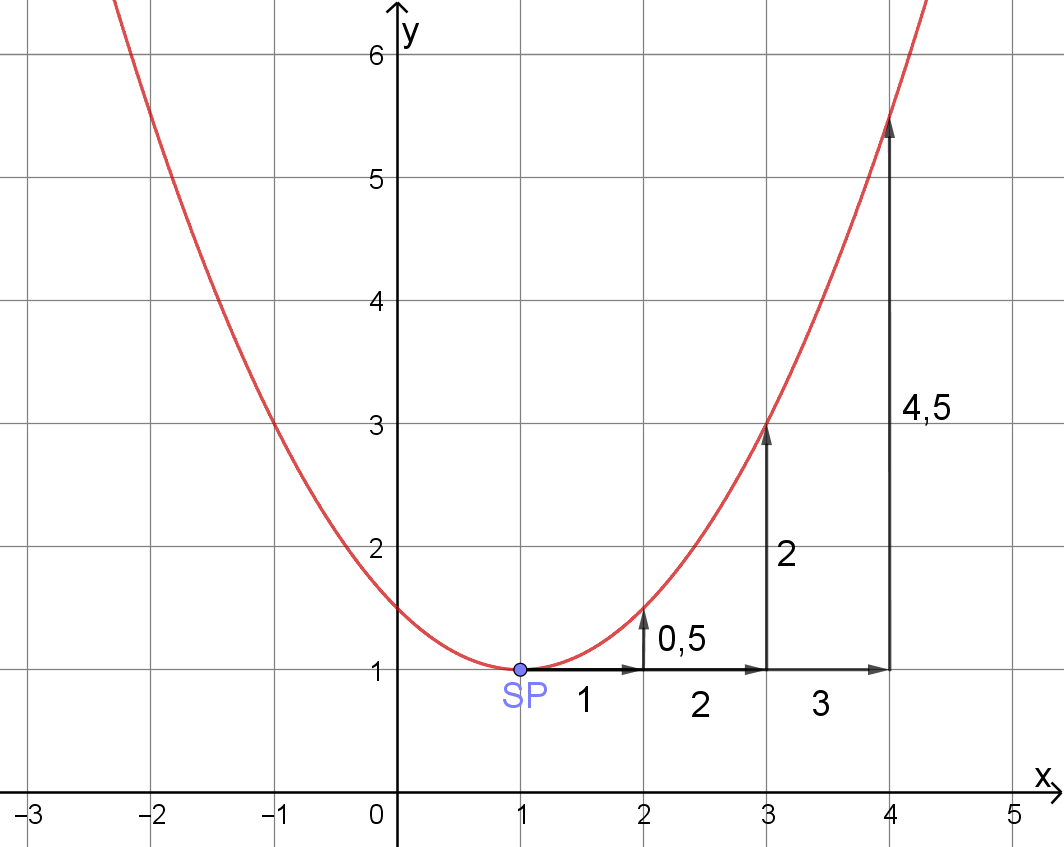
Die dargestellte Parabel hat einen Streckfaktor von $ a=\frac{1}{2} $.

Sieh dir die drei Schrittfolgen mit den dazugehörigen Längenpaaren $ \Delta x $ und $ \Delta y $  an.

Überlege, wie man aus den jeweiligen Lägenpaaren $ \Delta x $ und $ \Delta y $ jeweils den Streckfaktor $ a=\frac{1}{2} $ ermitteln kann.

Den Streckfaktor $ a=\frac{1}{2} $ erhält man, wenn man für die jeweiligen Längenpaare $ \frac{\Delta y}{(\Delta x)^2} $ berechnet.

 $ a=\frac{0,5}{1^2}= \frac{1}{2} $ 

 $ a=\frac{2}{2^2}= \frac{1}{2} $ 

 $ a=\frac{4,5}{3^2}= \frac{1}{2} $ 

usw.